5.2 The Definite Integral
In the previous section, we saw that if \(f(x)\) is continuous on an interval \([a,b]\), then the left-endpoint and right-endpoint approximations approach a common limit \(L\) as \(N \rightarrow \infty\):
\[L= \lim \limits_{N \rightarrow \infty} R_N = \lim \limits_{N \rightarrow \infty} L_N \tag {1}\]
300
When \(f(x) \geq 0,L\) is the area under the graph of \(f(x)\). In a moment, we will state formally that \(L\) is the definite integral of \(f(x)\) over \([a,b]\). Before doing so, we introduce more general approximations called Riemann sums.
Recall that \(R_N, L_N\) and \(M_N\) use rectangles of equal width \(\Delta x\), whose heights are the values of \(f(x)\) at the endpoints or midpoints of the subintervals. In Riemann sum approximations, we relax these requirements: The rectangles still have equal width, but the height may be any value of \(f(x)\) within the subinterval.
To specify a Riemann sum, we choose a partition and a set of sample points:
- Partition \(P\) of size \(N\): a choice of points that divides [a, b] into N subintervals of equal width \(\Delta x\): \[P: a=x_0 < x_1 < x_2 < \cdots < x_N=b \ \mbox{with} \ \Delta x = x_i-x_{i-1}=\frac{b-a}{N}\]
- Sample points \(X^*= \{x_1^*, x_2^*, \ldots,x_N^* \}\): \(x_i^*\) belongs to the subinterval \([x_{i-1},x_i]\) for all \(i\).
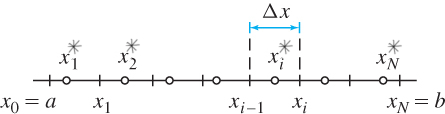
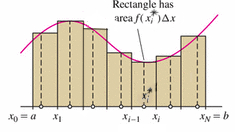
Given \(P\) and \(X^*\), we construct the rectangle of height \(f(x_i^*)\) and base \(\Delta x\) over each subinterval \([x_{i-1},x_i]\), as shown in the Figure 5.16 above. This rectangle has area \(f(x_i^*) \Delta x\) if \(f(x_i^*)\geq 0\). If \(f(x_i^*) <0\), the rectangle extends below the \(x\)-axis, and \(f(x_i^*) \Delta x\) is the negative of its area. The Riemann sum is the sum
\[\mbox{Rie}_N(f,X^*)=\sum_{i=1}^N f(x_i^*) \Delta x = f(x_1^*) \Delta x+f(x_2^*) \Delta x+ \cdots + f(x_N^*) \Delta x \tag {2}\]
EXAMPLE 1
Calculate \(\mbox{Rie}_N(f, X^*)\), where\(f(x) = 8+ 12 \sin x -4x\) on \([0,4]\), \(N=4\) and \(X^*=\{0.4,1.2,2,3.5\}\)
Solution The widths of the subintervals \(\Delta x\) in the partition are \(\Delta x=1\).
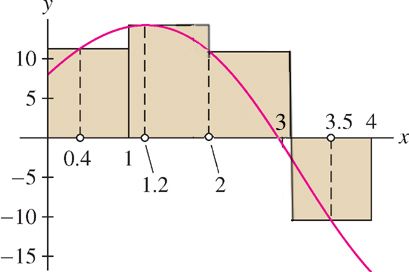
301
Using a calculator, we obtain
\[ \begin{array}{ccl} \mbox{Rie}_4(f, X^*) & = & f(0.4) \Delta x+f(1.2) \Delta x+ f(2) \Delta x+f(3.5) \Delta x \\ & \approx & 11.07 (1) +14.38 (1) + 10.91 (1) -10.2 (1) \\ & = & 26.16 \end{array}\]
DEFINITION Definite Integral
The definite integral of \(f(x)\) over \([a,b]\), denoted by the integral sign, is the limit of Riemann sums:
\[\int \limits_a^b f(x) \ dx= \lim_{N \rightarrow \infty} \mbox{Rie}_N (f, X^*)= \lim_{N \rightarrow \infty} \sum_{i=1}^Nf(x_i^*) \Delta x \]
When this limit exists, we say that \(f(x)\) is integrable over \([a,b]\).
The notation \( \int \limits_a^b f(x) \ dx\) was introduced by Leibniz in 1686. The symbol \(\int\) is an elongated S standing for “summation.” The differential \(dx\) corresponds to the length \(\Delta x\) along the \(x\)-axis.
The definite integral is often called, more simply, the integral of \(f(x)\) over \([a,b]\). The process of computing integrals is called integration. The function \(f(x)\) is called the integrand. The endpoints \(a\) and \(b\) of \([a,b]\) are called the limits of integration. Finally, we remark that any variable may be used as a variable of integration (this is a “dummy” variable). Thus, the following three integrals all denote the same quantity:
\[\int \limits_a^b f(x) \ dx, \hspace{10pt} \int \limits_a^b f(t) \ dt, \hskip 10pt \int \limits_a^b f(u) \ du \]
CONCEPTUAL INSIGHT
Keep in mind that a Riemann sum \(\mbox{Rie}_N(f,X^*)\) is nothing more than an approximation to area based on rectangles, and that \( \int \limits_a^b f(x) \ dx\) is the number we obtain in the limit as we take thinner and thinner rectangles.
However, general Riemann sums (with arbitrary partitions and sample points) are rarely used for computations. In practice, we use particular approximations such as \(R_N\) and \(L_N\), or the Fundamental Theorem of Calculus, as we’ll learn in the next section. If so, why bother introducing Riemann sums? The answer is that Riemann sums play a theoretical rather than a computational role. They are useful in proofs and for dealing rigorously with certain discontinuous functions. In later sections, Riemann sums are used to show that volumes and other quantities can be expressed as definite integrals.
The next theorem assures us that continuous functions (and even functions with finitely many jump discontinuities) are integrable (see Appendix D for a proof). In practice, we rely on this theorem rather than attempting to prove directly that a given function is integrable.

One of the greatest mathematicians of the nineteenth century and perhaps second only to his teacher C. F. Gauss, Riemann transformed the fields of geometry, analysis, and number theory. Albert Einstein based his General Theory of Relativity on Riemann’s geometry. The “Riemann hypothesis” dealing with prime numbers is one of the great unsolved problems in present-day mathematics. The Clay Foundation has offered a $1 million prize for its solution (https://www.claymath.org/millennium).
302
THEOREM 1
If \(f(x)\) is continuous on \([a,b]\), or if \(f(x)\) is continuous with at most finitely many jump discontinuities, then \(f(x)\) is integrable over \([a,b]\).
Interpretation of the Definite Integral as a Sum and Difference of Areas
When \(f(x) \geq 0\), the definite integral defines the area under the graph. To interpret the integral when \(f(x)\) takes on both positive and negative values, we can informally consider regions below the \(x\)-axis to have “negative area” (see Figure 5.18 below).
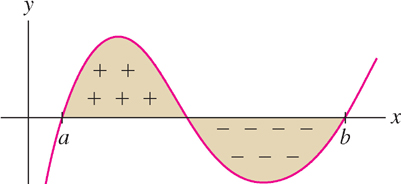
Now observe that a Riemann sum is equal to the sums and differences of the areas of the corresponding rectangles:
\[\mbox{Rie}_N(f,X^*)=\sum_{i=1}^N f(x_i^*) \Delta x = f(x_1^*) \Delta x+f(x_2^*) \Delta x+ \cdots + f(x_N^*) \Delta x\]
Indeed, if \(f(x_i^*) < 0\), then the corresponding rectangle lies below the \(x\)-axis and the quantity \(f(x_i^*) \Delta x\) has value equal to the negative of the area of this rectangle (see the dynamic Figure 5.19 below).

The limit of the Riemann sums is the sum and difference of the areas of the region between the graph and the x-axis:
\begin{equation} \boxed{\bbox[#FAF8ED,5pt]{\int \limits_a^b f(x) \ dx = \mbox{(area above the \(x\)-axis)-(area below the \(x\)-axis)}}} \end{equation}
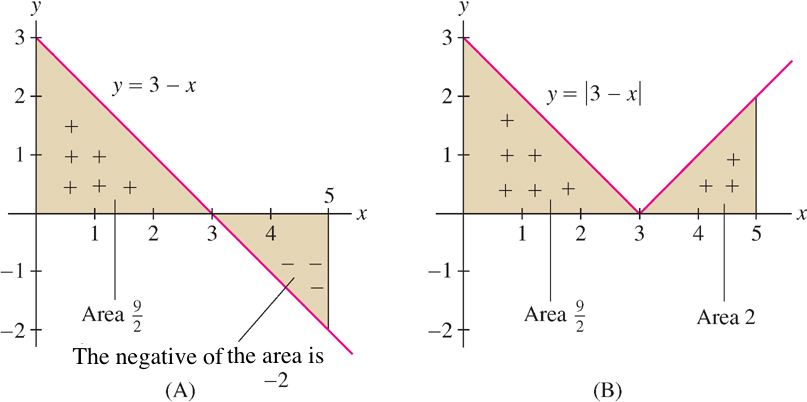
EXAMPLE 2
Calculate
\[ \int \limits_0^5 (3-x) \ dx \hskip 10pt \mbox{and} \hskip 10pt \int \limits_0^5 |3-x| \ dx \]
Solution The region between \(y=3-x\) and the \(x\)-axis consists of two triangles of areas \(\frac92\) and 2 [see the Figure 5.20A and Figure 5.20B below]. However, the second triangle lies below the \(x\)-axis. In the graph of \(y=|3-x|\), both triangles lie above the x-axis. Therefore,
\[ \int \limits_0^5 (3-x) \ dx = \frac92-2 = \frac52 \hskip 10pt \mbox{and} \hskip 10pt \int \limits_0^5 |3-x| \ dx = \frac92+2 = \frac{13}{2}\]
Question 5.7 Definite Integral Progress Check Question 1
Calculate
\[ \int \limits_1^5 (2-x) \ dx \]
303
Properties of the Definite Integral
In the rest of this section, we discuss some basic properties of definite integrals. First, we note that the integral of a constant function \(f(x) = c\) over \([a,b]\), is either the area or the negative of the area of a rectangle (see figure below).
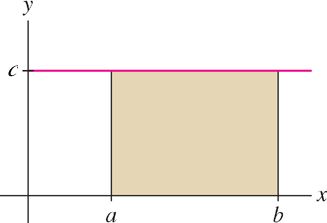
THEOREM 2 Integral of a Constant
For any constant \(c\), \[\int \limits_a^b c \ dx= c(b-a) \tag{4}\]
Question 5.8 Definite Integral Progress Check Question 2
Calculate
\[ \int \limits_{-3}^1 -2\ dx \]
Next, we state the linearity properties of the definite integral.
THEOREM 3 Linearity of the Definite Integral
If \(f\) and \(g\) are integrable over \([a,b]\), then \(f+g\) and \(cf\) are integrable over \([a,b]\) (for any constant \(c\)), and
- \[\int \limits_a^b \big(f(x)+g(x)\big) \ dx= \int \limits_a^b f(x) \ dx+ \int \limits_a^b g(x) \ dx\]
- \[\int \limits_a^b c f(x) \ dx= c \int \limits_a^b f(x) \ dx\]
Proof
These properties follow from the corresponding linearity properties of sums and limits. For example, Riemann sums are additive:
\[\begin{array}{ccl} \mbox{Rie}_N(f+g,X^*) & = & \sum_{i=1}^N \big(f(x_i^*)+g(x_i^*)\big) \Delta x \\ & = & \sum_{i=1}^N f(x_i^*) \Delta x+ \sum_{i=1}^N g(x_i^*) \Delta x \\ & = & \mbox{Rie}_N(f,X^*)+ \mbox{Rie}_N(g,X^*) \end{array}\]
By the additivity of limits,
\[\begin{array}{ccl} \int \limits_a^b \big(f(x)+g(x)\big) \ dx & = & \lim_{N \rightarrow \infty} \mbox{Rie}_N(f+g,X^*) \\ & = & \lim_{N \rightarrow \infty} \mbox{Rie}_N(f,X^*) + \lim_{N \rightarrow \infty} \mbox{Rie}_N(g,X^*) \\ & = & \int \limits_a^b f(x) \ dx+ \int \limits_a^b g(x) \ dx \end{array}\]
The second property is proved similarly.
EXAMPLE 3
Calculate \(\int \limits_0^3 (2x^2-5) \ dx\) using the formula
\begin{equation} \boxed{\bbox[#FAF8ED,5pt]{ \int \limits_0^b x^2 \ dx = \frac{b^3}{3} }}\tag {5} \end{equation}
Solution
\[ \begin{array}{ccll} \int \limits_0^3 (2x^2-5) \ dx & = & 2 \int \limits_0^3 x^2 \ dx + \int \limits_0^3 (-5) \ dx & \mbox{(linearity)} \\ & = & 2 \Big(\frac{3^3}{3}\Big) - 5 (3-0) = 3 & \mbox{[Eqs (5) and (4)]} \end{array}\]
Eq. (5) was verified in Example 5 of Section 5.1.
304
So far we have used the notation \(\int \limits_a^b f(x) \ dx \) with the understanding that \(a<b\). It is convenient to define the definite integral for arbitrary \(a\) and \(b\).
DEFINITION Reversing the Limits of Integration
For \(a < b\), we set
\[ \boxed{\bbox[#FAF8ED,5pt]{\int \limits_a^b f(x) \ dx = - \int \limits_b^a f(x) \ dx}}\tag {6} \]
According to Eq. (6), the integral changes sign when the limits of integration are reversed. Since we are free to define symbols as we please, why have we chosen to put the minus sign in Eq. (6)? Because it is only with this definition that the Fundamental Theorem of Calculus holds true.
For example, by Def. (6) and Eq. (5),
\[\int \limits_5^0 x^2 \ dx = -\int \limits_0^5 x^2 \ dx = -\frac{5^3}{3}=-\frac{125}{3}\]
When \(a=b\), the interval \([a,b]=[a,a]\) has length zero and we define the definite integral to be zero:
\[ \boxed{\bbox[#FAF8ED,5pt]{\int \limits_a^a f(x) \ dx = 0}} \]
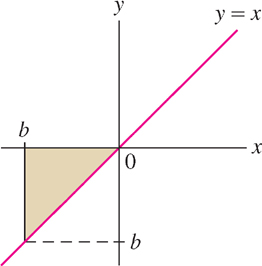
EXAMPLE 4
Prove that, for all \(b\) (positive or negative),
\[ \boxed{\bbox[#FAF8ED,5pt]{\int \limits_0^b x \ dx = \frac12 b^2}} \tag{7} \]
Solution If \(b>0, \int \limits_0^b x \ dx\) is the area \(\frac12 b^2\) of a triangle of base \(b\) and height \(b\). If \(b <0, \int \limits_b^0 x \ dx\) is the negative of the area of the triangle, namely \(-\frac12 b^2\) as you can see in Figure 5.22 below, and Eq. (7) follows from the rule for reversing limits of integration:
\[\int \limits_0^b x \ dx = -\int \limits_b^0 x \ dx = -\Big(-\frac12 b^2 \Big)= \frac12 b^2\]
Question 5.9 Definite Integral Progress Check Question 3
Calculate
\[ \int \limits_1^0 (2x-9x^2) \ dx \]
Definite integrals satisfy an important additivity property: If \(f(x)\)is integrable and \(a \leq b \leq c\) as in Figure 5.23 below, then the integral from \(a\) to \(c\) is equal to the integral from \(a\) to \(b\) plus the integral from \(b\) to \(c\). We state this in the next theorem (a formal proof can be given using Riemann sums).
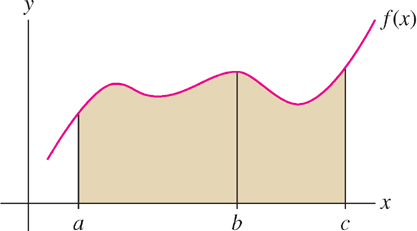
THEOREM 4 Additivity for Adjacent Intervals
Let \(a \leq b \leq c\), and assume that \(f(x)\) is integrable. Then
\[\int \limits_a^c f(x) \ dx = \int \limits_a^b f(x) \ dx+ \int \limits_b^c f(x) \ dx\]
This theorem remains true as stated even if the condition \(a \leq b \leq c\) is not satisfied.
EXAMPLE 5
Calculate \(\int \limits_4^7 x^2 \ dx\).
Solution Before we can apply the formula \(\int \limits_0^b x^2 \ dx = \dfrac{b^3}{3} \) from Example 3, we must use the additivity property for adjacent intervals to write
\(\int \limits_0^4 x^2 \ dx + \int \limits_4^7 x^2 \ dx = \int \limits_0^7 x^2 \ dx\)
305
Now we can compute our integral as a difference:
\(\int \limits_4^7 x^2 \ dx=\int \limits_0^7 x^2 \ dx-\int \limits_0^4 x^2 \ dx = \Big(\dfrac13\Big)7^3-\Big(\dfrac13\Big) 4^3=93\)
Question 5.10 Definite Integral Progress Check Question 4
Calculate
\[ \int \limits_1^2 3x^2 \ dx \]
Another basic property of the definite integral is that larger functions have larger integrals (Figure 5.24).
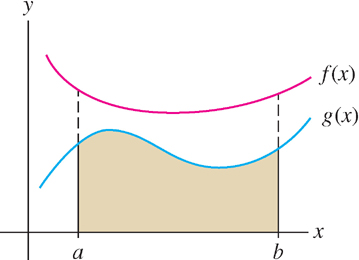
THEOREM 5 Comparison Theorem
If \(f\) and \(g\) are integrable and \(g(x) \leq f(x)\) for \(x\) in \([a,b]\), then
\[\int \limits_a^b g(x) \ dx \leq \int \limits_a^b f(x) \ dx\]
Proof
If \(g(x) \leq f(x)\), then for any partition and choice of sample points, we have \(g(x_i^*) \Delta x \leq f(x_i^*) \Delta x\) for all \(i\). Therefore, the Riemann sums satisfy
\[\sum \limits_{i=1}^N g(x_i^*) \Delta x \leq \sum \limits_{i=1}^N f(x_i^*) \Delta x\]
Taking the limit as \(N\) tends to \(\infty\), we obtain
\[\int \limits_a^b g(x) \ dx = \lim \limits_{N \rightarrow \infty} \sum \limits_{i=1}^N g(x_i^*) \Delta x \leq \lim \limits_{N \rightarrow \infty} \sum \limits_{i=1}^N f(x_i^*) \Delta x = \int \limits_a^b f(x) \ dx\]
EXAMPLE 6
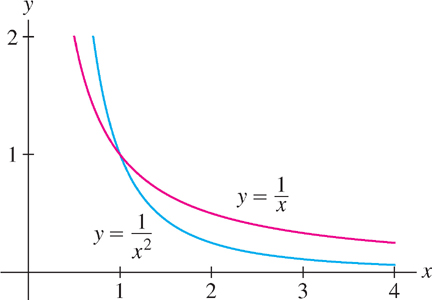
Prove the inequality: \[\int \limits_1^4 \dfrac{1}{x^2} \ dx \leq \int \limits_1^4 \dfrac{1}{x} \ dx \]
Solution If \(x \geq 1\), then \(x^2 \geq x\), and \(\dfrac{1}{x^2} \leq \dfrac{1}{x}\) [see the figure below]. Therefore, the inequality follows from the Comparison Theorem, applied with \(g(x) = \dfrac{1}{x^2}\) and \(f(x) = \dfrac{1}{x}\).
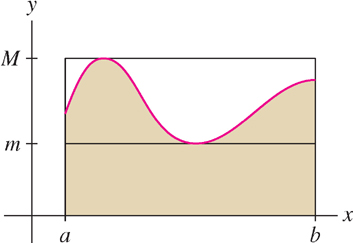
Suppose there are numbers \(m\) and \(M\) such that \(m \leq f(x) \leq M \) for \(x\) in \([a,b]\). We call \(m\) and \(M\) lower and upper bounds for \(f(x) \) on \([a,b]\). By the Comparison Theorem,
\[\int \limits_a^b m \ dx \leq \int \limits_a^b f(x) \ dx \leq \int \limits_a^b M \ dx\]
and thus
\[ \boxed{\bbox[#FAF8ED,5pt]{m(b-a) \leq \int \limits_a^b f(x) \ dx \leq M (b-a)}} \tag{8}\]
This says simply that the integral of \(f(x)\) lies between the areas of two rectangles (see figure below).
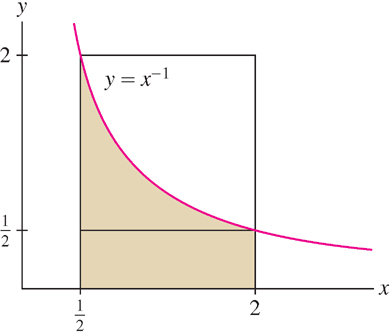
EXAMPLE 7
Prove the inequalities: \[\dfrac34 \leq \int \limits_{\frac12}^2 \dfrac1x \ dx \leq 3\]
Solution Because \(f(x) = \dfrac1x\) is decreasing (see figure below), its minimum value on \([\frac12,2]\) is \(m=f(2)=\dfrac12\) and its maximum value is \(M= f(\frac12)=2\). By Eq. (8),
\[ \underbrace{\dfrac12(2-\dfrac12)}_{m(b-a)} = \dfrac34 \leq \int \limits_{\frac12}^2 \dfrac1x \ dx \leq \underbrace{2(2-\dfrac12)}_{M(b-a)} =3\]
Question 5.11 Definite Integral Progress Check Question 5
True or False? \[ \int \limits_2^4 e^x \ dx > \int \limits_2^4 3 \ dx \]
| A. |
| B. |
| C. |
306
5.2.1 Summary
- A Riemann sum \( \mbox{Rie}_N(f, X^*)\) for the interval \([a,b]\) is defined by choosing a partition \(P: a=x_0 < x_1 < x_2 < \cdots < x_N=b\) with \(\Delta x = \frac{b-a}{N}\) and sample points \(X^*=\{x_1^*, x_2^*, \cdots, x_N^*\}\) where \(x_i^* \in [x_{i-1},x_i]\). Then \( \mbox{Rie}_N(f, X^*) = \sum \limits_{i=1}^N f(x_i^*) \Delta x\)
- The definite integral is the limit of the Riemann sums (if it exists): \(\int \limits_a^b f(x) \ dx = \lim \limits_{N \rightarrow \infty} \mbox{Rie}_N(f, X^*)\). We say that \(f(x)\)is integrable over \([a.b]\) if the limit exists.
- Theorem: If \(f(x)\) is continuous on \([a,b]\), then \(f(x)\) is integrable over \([a,b]\).
- \(\int \limits_a^b f(x) \ dx\) = area of the region between the graph of \(f(x)\) above the \(x\)-axis minus that below.
- Properties of definite integrals: \[\int \limits_a^b \big(f(x)+g(x)\big) \ dx= \int \limits_a^b f(x) \ dx+ \int \limits_a^b g(x) \ dx\] \[\int \limits_a^b c f(x) \ dx= c \int \limits_a^b f(x) \ dx\] \[\int \limits_a^b f(x) \ dx = - \int \limits_b^a f(x) \ dx \] \[\int \limits_a^a f(x) \ dx =0\] \[\int \limits_a^b f(x) \ dx + \int \limits_b^c f(x) \ dx = \int \limits_a^c f(x) \ dx\]
- Formulas: \[\int \limits_a^b c \ dx= c(b-a) \hskip 10pt \mbox{(\(c\) any constant)}\] \[\int \limits_0^b x \ dx = \dfrac12 b^2 \] \[\int \limits_0^b x^2 \ dx = \dfrac13 b^3 \]
- Comparison Theorem: If \(f(x) \leq g(x)\) on \([a,b]\), then \[\int \limits_a^b f(x) \ dx \leq \int \limits_a^b g(x) \ dx\]
- If \(m \leq f(x) \leq M \) on \([a,b]\), then \[m(b-a) \leq \int \limits_a^b f(x) \ dx \leq M (b-a)\]
307